Extreme value theory is concerned with the modelling and prediction of extremes in a series of observations. Accurate estimates of probabilities for the exceedence of extreme levels of temperature, financial loss, the number of defective nodes in a network etc. are crucial for the control of risk in a great number of societal systems. “Mainstream” extreme value theory assumes that events happen uniformly, e.g. yearly, daily, or every second, or that events occur at a certain rate (Poisson process). In fact, however, a great number of systems violates this assumption: Events occur in Bursts, intermittent with quiescent periods drawn from a heavy-tailed distribution. This phenomenon is ubiquitous for human-created events, and is deemed to occur for any type of action resulting from a dynamic list of priorities.
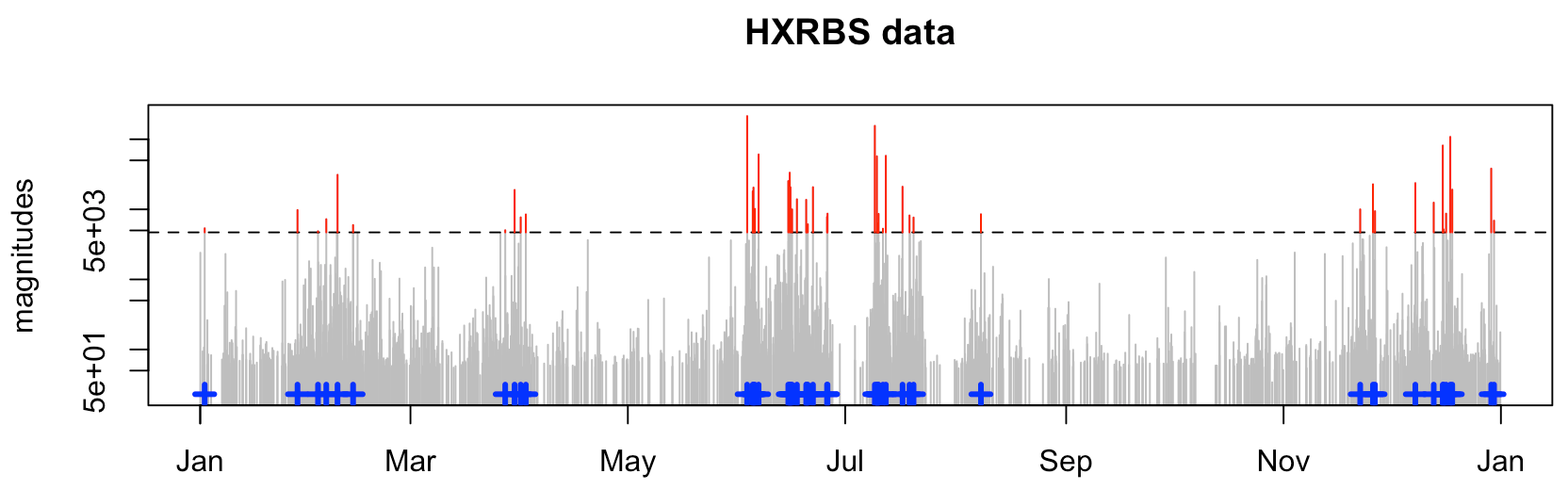
Often a magnitude, or mark can be assigned to each event in the renewal process, such as for earthquakes, solar flares, neuron voltages etc. The Peaks-Over-Threshold model (POT, see e.g. Coles 2001) applies a threshold to the magnitudes, and fits a Generalized Pareto distribution to the threshold exceedances. The timing of the threshold exceedances fits well with a “Poisson process”, i.e. the threshold crossing times are distributed completely randomly on the given time interval.
For bursty data, the Poisson process representation is no long valid, but a fractional Poisson process representation holds. This project derives the theoretical model behind the timings of bursty threshold crossings, statistical methods for the fitting of the model, and R software packages for applications to data.