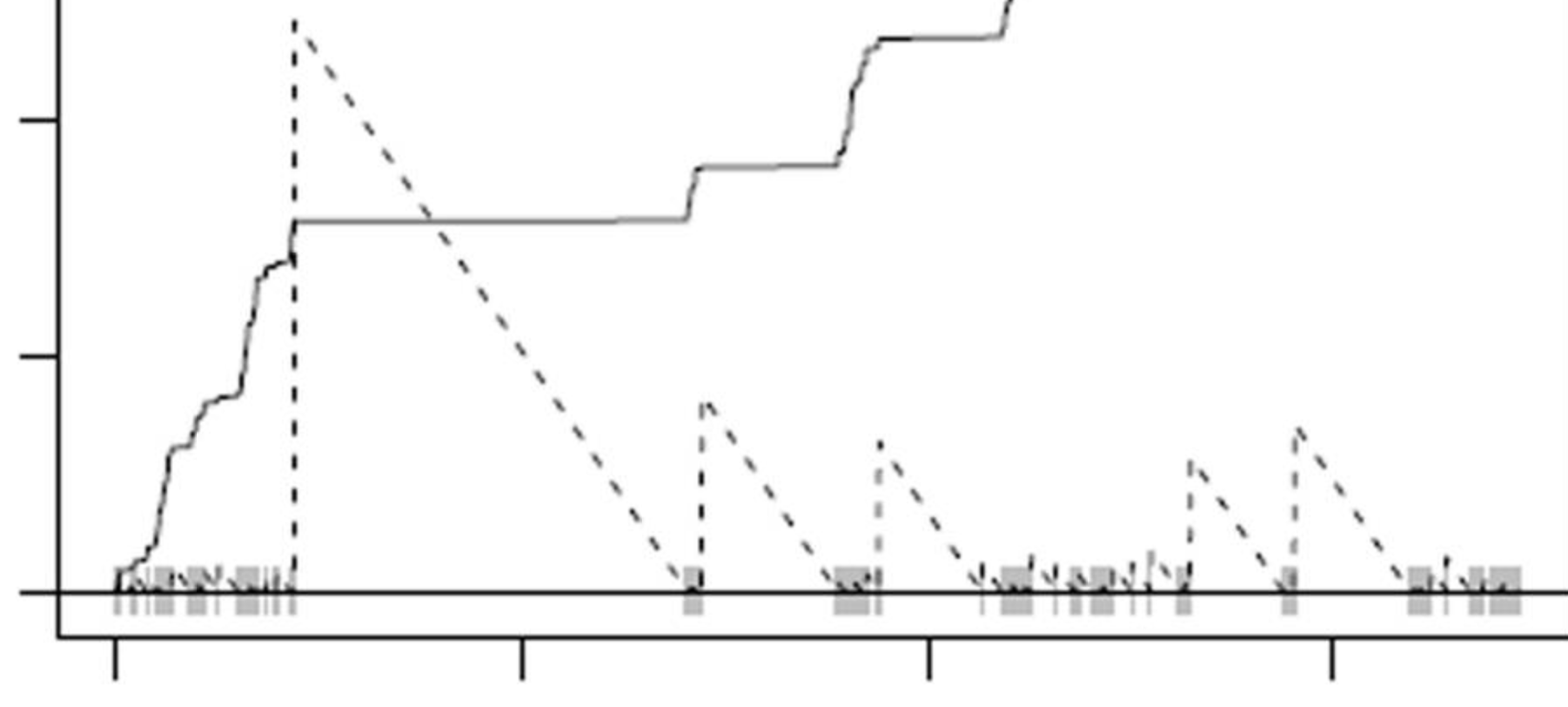
 Renewal process and forward recurrence time
Renewal process and forward recurrence time
Fractional Dynamics at Multiple Times
Abstract
A continuous time random walk (CTRW) imposes a random waiting time between random particle jumps. CTRW limit densities solve a fractional Fokker-Planck equation, but since the CTRW limit is not Markovian, this is not sufficient to characterize the process. This paper applies continuum renewal theory to restore the Markov property on an expanded state space, and compute the joint CTRW limit density at multiple times.
Type
Publication
Journal of Statistical Physics. Volume 149, Issue 5, pp 878–886
Date
November, 2012