Peaks Over Threshold for Bursty Time Series
Abstract
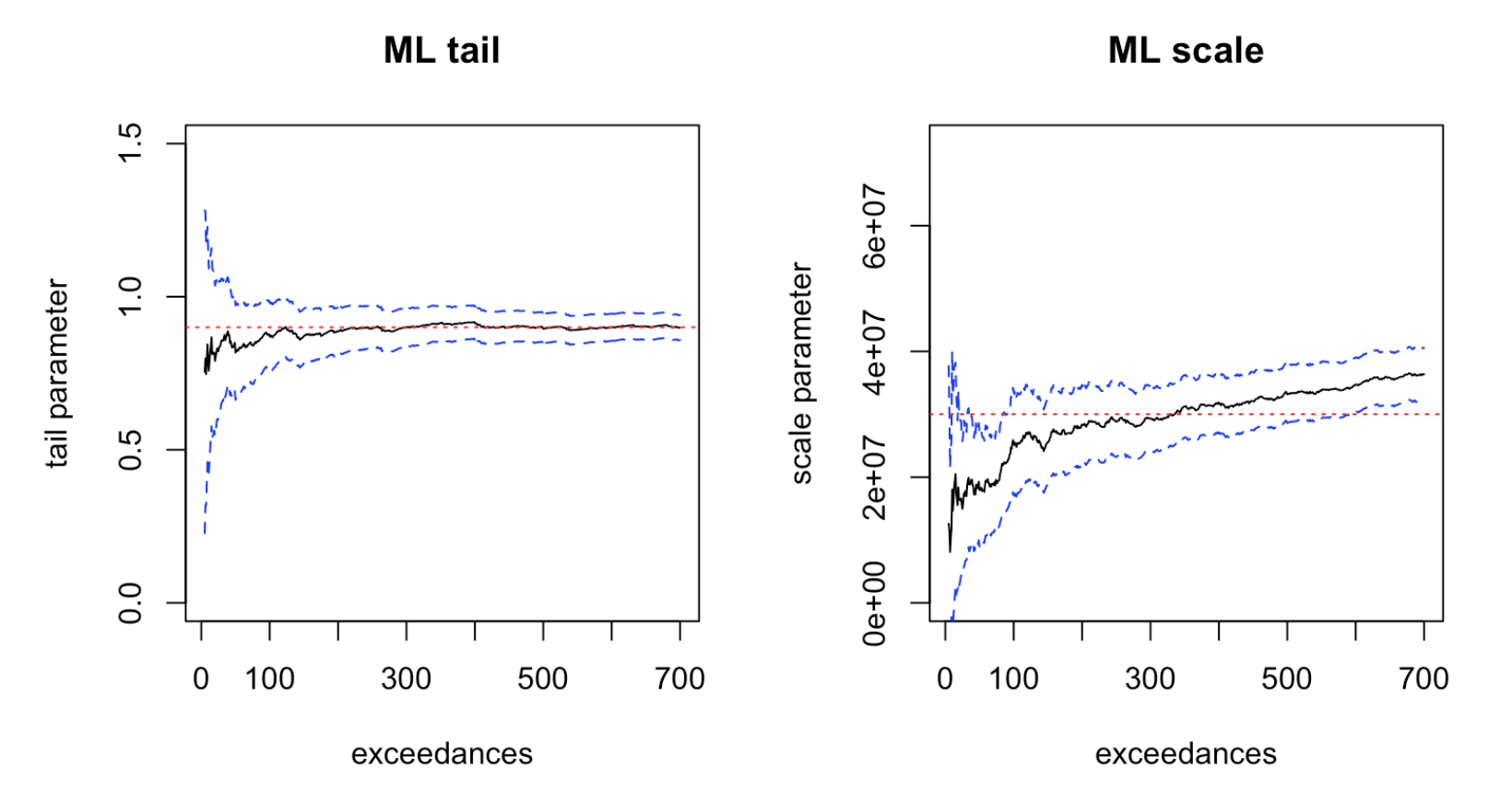
In many complex systems studied in statistical physics, inter-arrival times between events such as solar flares, trades and neuron voltages follow a heavy-tailed distribution. The set of event times is fractal-like, being dense in some time windows and empty in others, a phenomenon which has been dubbed ‘bursty’. This article generalizes the Peaks Over Threshold (POT) model to the setting where inter-event times are heavy-tailed. For high thresholds and infinite-mean waiting times, we show that the times between threshold crossings are Mittag-Leffler distributed, and thus form a ‘fractional Poisson Process’ which generalizes the standard Poisson Process. We provide graphical means of estimating model parameters and assessing model fit. Along the way, we apply our inference method to a real-world bursty time series, and show how the memory of the Mittag-Leffler distribution affects the predictive distribution for the time until the next extreme event.