The new paper (arxiv.org/abs/1712.06767)
Variable Order Fractional Fokker-Planck Equations derived from Continuous Time Random Walks
is currently under review.
The variable order fractional Fokker-Planck equation (VOFFPE), in simple form1, is \[\frac{\partial}{\partial t} p(x,t) = \frac{\partial^2}{\partial x^2} \underbrace{D_t^{1-\beta(x)}}_{\text{fractional derivative}} p(x,t).\]
- If you take out the fractional derivative operator, you get the Fokker-Planck equation (FPE). It describes the spreading of probability via a random walk:
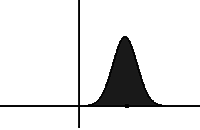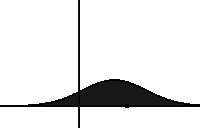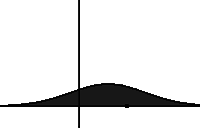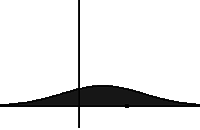
Adding in the fractional derivative \[D_t^{1-\beta} p(x,t) = \int_0^t p(x,t-s) \frac{s^{-\beta}}{\Gamma(1-\beta)}\,ds\] results in the “fractional FPE”. The fractional derivative corresponds to longs rests of a walker, and slows down the spreading (making the dynamics “sub”diffusive).
Here the order \(1-\beta\) of the fractional derivative varies with the location \(x\) of the walker, hence the name VOFFPE (variable order fractional FPE). In some regions, e.g. where the intracellular matrix of a cell is dense2, the trappingness can be stronger, which is modelled by a smaller \(\beta(x)\) in that region.
The paper shows that the equation has a unique solution \(p(x,t)\), and that this solution is the probability distribution of a Continuous Time Random Walk (CTRW)3. CTRWs are random walks with random waiting times between jumps:
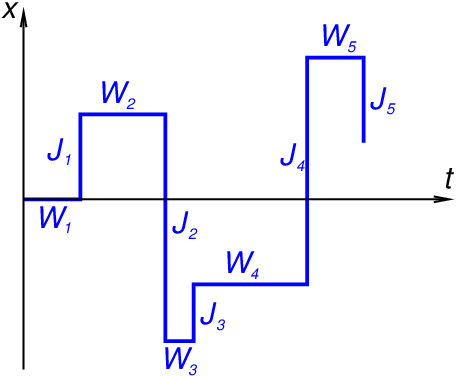
The fractional derivative in time is tightly linked with Mittag-Leffler distributed waiting times.
Of course CTRWs can be simulated, and \(p(x,t)\) may be computed via Monte Carlo simulations (or “particle tracking”). Thus a consequence of the paper is the mathematical certainty that the variable order FFPE (VOFFPE) can be solved by simulations.
The variable order FFPE can also be solved directly, via clever numerical algorithms. The CTRW interpretation of the VOFFPE can be leveraged for such a clever numerical algorithm, as our friends over in applied maths have done with their Discrete Time Random Walk algorithm. This approach has several great benefits4, and now we know how to extend these benefits to the variable order setting (to be continued).